Turing machines
From 2009.igem.org
| Line 37: | Line 37: | ||
0 | 0 | ||
| - | The above is a sample of such a ‘tape’ which is fed to the machine. For simplicity of demonstration and argument we have labeled the tape in only two ways viz. 0 and 1. Turing allowed more complex markings but that shouldn’t bother us here. | + | The above is a sample of such a ‘tape’ which is fed to the machine. For simplicity of demonstration and argument we have labeled the tape in only two ways viz. 0 and 1. |
| + | |||
| + | Turing allowed more complex markings but that shouldn’t bother us here. | ||
Coming back to the box, as we have seen that the box can move the tape, change its marks etc. but it should be noted that the machine does these operations in a non-random, deterministic way. That is we can predict what the action of the Turing machine on the tape will be. The box has a set of finite internal states, but can work algorithmically on potentially infinite calculations or specifications of the tape. | Coming back to the box, as we have seen that the box can move the tape, change its marks etc. but it should be noted that the machine does these operations in a non-random, deterministic way. That is we can predict what the action of the Turing machine on the tape will be. The box has a set of finite internal states, but can work algorithmically on potentially infinite calculations or specifications of the tape. | ||
Revision as of 12:02, 6 July 2009
Turing machines form an extremely exciting part of mathematics, yes; they are a piece of mathematics which are elegant, simple and powerful. They form the basis of computer programming. They help us understand the nature of algorithms and how the mind works.
Let us first try to see what a Turing machine actually is. The scientist and brilliant mathematician Alan Turing came up with this idea in an attempt to solve a problem in mathematics known as Entscheidungsproblem. It translates to "a decision problem", and it was put forward by the German mathematician David Hilbert. Hilbert’s problem was- is there any general algorithmic procedure for resolving mathematical questions or whether in principle such a procedure might exist.
Turing’s concept:
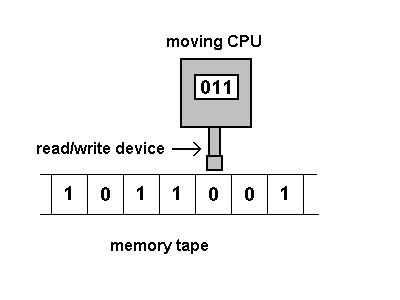
Turing’s machine consisted of a box capable of performing the following actions on a tape supplied to it:
It can ‘read’ the marks on the tape,
It can erase the marks on the tape or can change the marks on the existing tape,
It can move the tape towards the right or left, allowing it to ‘read’ further marks on the tape.
0 0 0 0 1 1 0 1 1 1 1 0 1 0 1 0 0 0 1 0
The above is a sample of such a ‘tape’ which is fed to the machine. For simplicity of demonstration and argument we have labeled the tape in only two ways viz. 0 and 1.
Turing allowed more complex markings but that shouldn’t bother us here.
Coming back to the box, as we have seen that the box can move the tape, change its marks etc. but it should be noted that the machine does these operations in a non-random, deterministic way. That is we can predict what the action of the Turing machine on the tape will be. The box has a set of finite internal states, but can work algorithmically on potentially infinite calculations or specifications of the tape.
REFERENCES
1. http://en.wikipedia.org/wiki/Turing_machine
 "
"