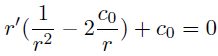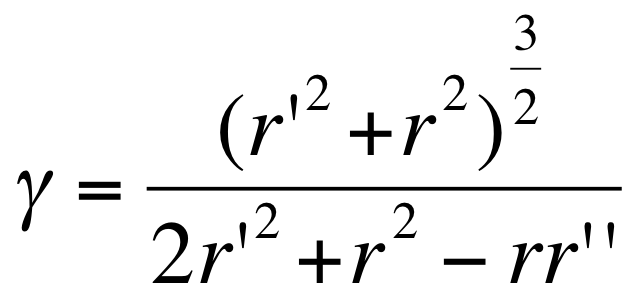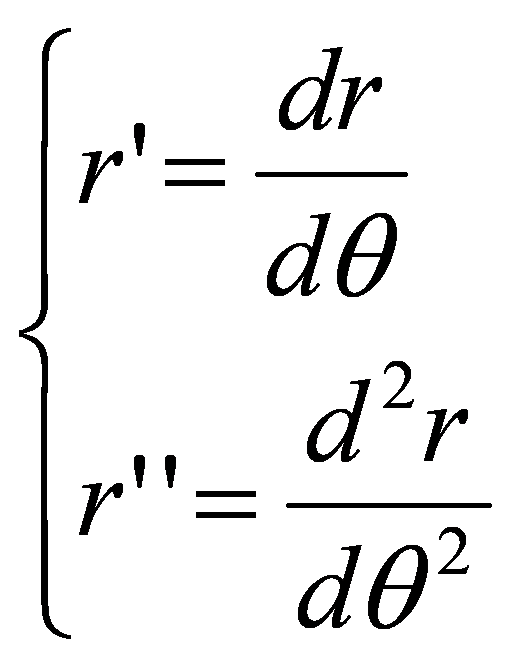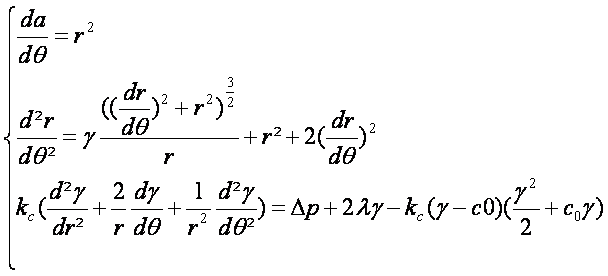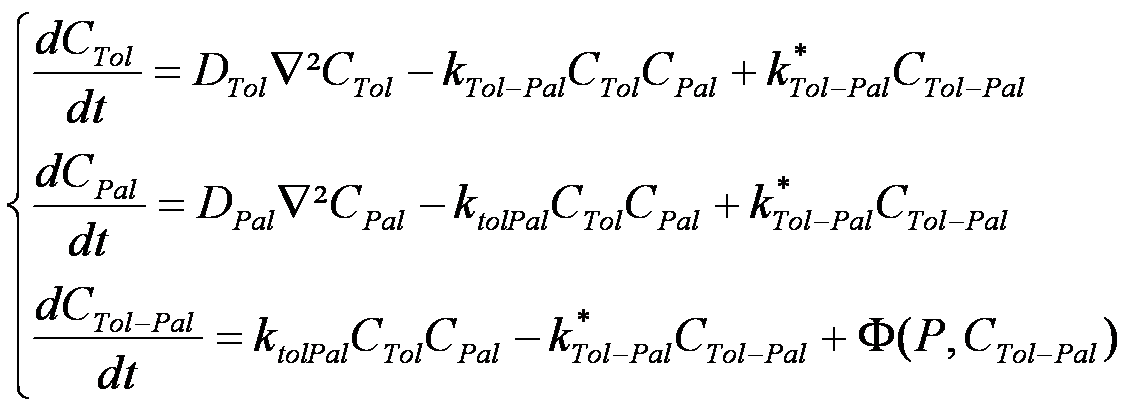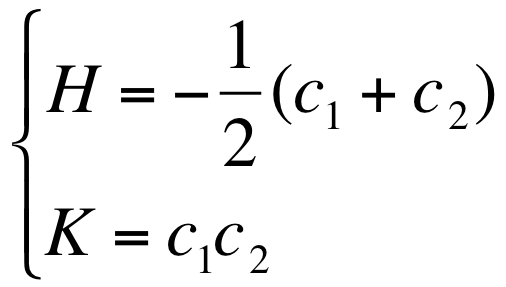Team:Paris/Production modeling2
From 2009.igem.org
Gregory Batt (Talk | contribs) (→Modeling Tol/Pal diffusion) |
Gregory Batt (Talk | contribs) (→DryLab - Vesicles biophysics model) |
||
| Line 150: | Line 150: | ||
The main feature of our Tol/Pal diffusion model is that we take into account that '''diffusion''' may happen '''on non-flat surfaces''', and that the '''Tol/Pal complex is anchored''' both in the '''intracellular''' (Tol) and '''extracellular''' (Pal) '''membranes'''. | The main feature of our Tol/Pal diffusion model is that we take into account that '''diffusion''' may happen '''on non-flat surfaces''', and that the '''Tol/Pal complex is anchored''' both in the '''intracellular''' (Tol) and '''extracellular''' (Pal) '''membranes'''. | ||
We assumed that the intracellular membrane position is fixed (pushed against the peptidoglycan layer). | We assumed that the intracellular membrane position is fixed (pushed against the peptidoglycan layer). | ||
| - | |||
| - | |||
Revision as of 22:24, 21 October 2009
iGEM > Paris > DryLab > Vesicle biophysics Model (vesicle model)
Contents |
DryLab - Vesicles biophysics model
This part aims at investigating an important issue regarding the creation of vesicles:
What is the link between Tol/Pal expression and vesicle formation?
Or, more precisely, can we explain vesicle formation solely by the diffusion of the doubly anchored Tol/Pal complex in the membrane ?
Understanding this connection is instrumental, since our project relies on the hypothesis that an increased rate of vesicle formation can be obtained simply by destabilization of the Tol/Pal complexes.
To answer this question, we developed a biophysical model of the cellular membranes and Tol/Pal complexes, that incorporates outer membrane deformation and Tol/Pal diffusion in membranes by Brownian motion.
Our initial simulation results suggested a three-stage process for vesicle formation.
Thus, in what follows, we decomposed the original main question in three parts:
- Can we explain the formation of small blebs by differences of osmotic pressures between intra- and extra-cellular environments?
- Can we explain the accumulation of Tol/Pal molecules at the basis of nascent blebs?
- Can we explain vesiculation by constriction of blebs basis by accumulated Tol/Pal molecules?
Before answering these questions, we start by describing how we modeled membrane deformation and Tol/Pal diffusion.
The main features of our membrane model is that we take into account the presence of osmotic pressure differences between intra and extra cellular environments and the existence of an outer membrane intrinsic preferred curvature.
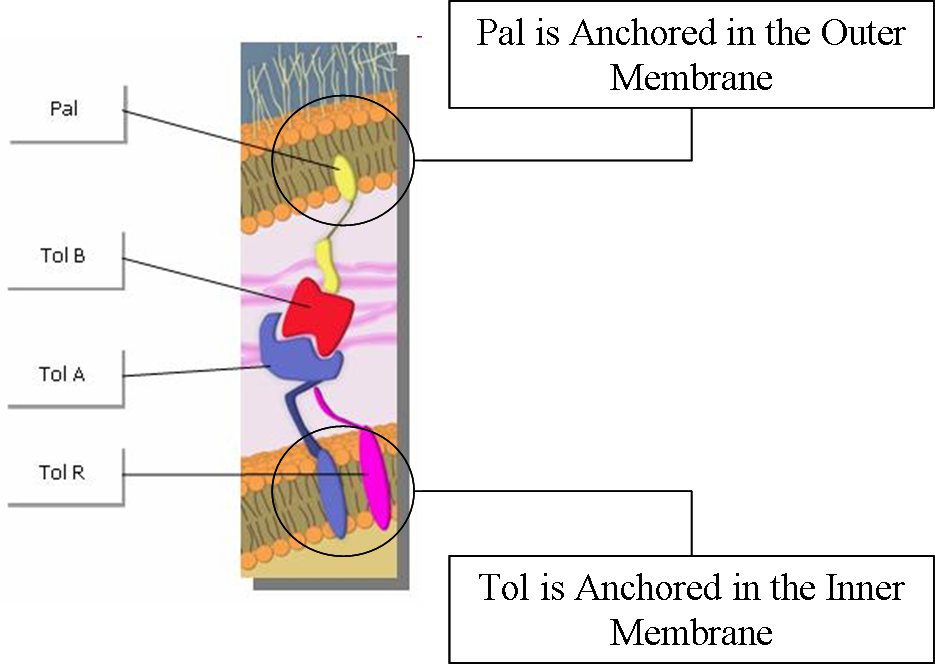
The main feature of our Tol/Pal diffusion model is that we take into account that diffusion may happen on non-flat surfaces, and that the Tol/Pal complex is anchored both in the intracellular (Tol) and extracellular (Pal) membranes.
We assumed that the intracellular membrane position is fixed (pushed against the peptidoglycan layer).
The lipid surface conformation
The Lipid conformation of the outer membrane is a well known problem: at 35°c the lipid bilayer behaves like a liquid which conformation character is ruled by an energy called the bending energy [1]. This energy represents the fact that the lipid bilayer will search a special conformation depending on the shape and the chemical properties of its constituents. In order to explain the way lipids organize together we need an expression for the membrane bending energy. This is given by :
E is the energy of a whole lipid bilayer (or monolayer). Kb and Kg are Bending and Gaussian moduli which can be obtained by experiments. γ0 is the intrinsic curvature of the outer membrane which describes the local form of a lipid bilayer when it is at is lowest state of energy ,the more stable. γm and Hg are the mean curvature and the gaussian curvature. dS is a surface infinitesimal element and the previous formula relates how the local surface energy varies with the local mean curvature and the Gaussian curvature. With this relation we can find an relationship beetween the radius of the more easilly created vesicles r', the radius of E.coli r and the γ0:
As we know that the range of created vesicles radii is 25 nm to 175nm we can suppose that the r’ is somehow about 100 nm. This leads us to an estimation of the outer membrane intrinsic curvature:
Which is realistic in the order of magnitude
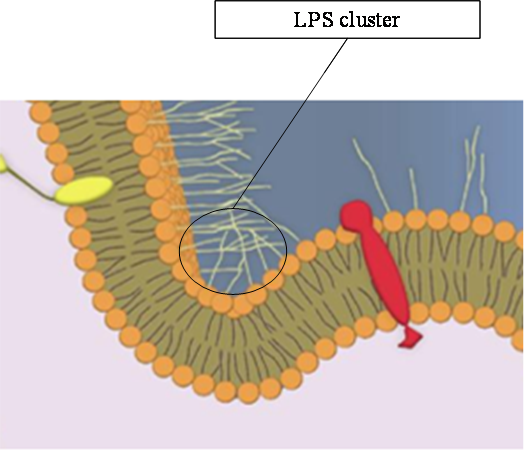
In fact we know that the E.coli lipid bilayer is built of distinct types of lipids: Lippopolysacharides (LPS) and simple phospholipids. LPS are located in the exterior lipid layer of the outer membrane. The others are located in the interior lipid bilayer. Moreover, those LPS present a sugar extension toward the medium. Those sugars can bind to each other. So we can assume that they are going to create clusters and to curve the membrane toward the exterior of E.coli.
Modeling membrane deformation
To obtain a reasonably simple model, we assumed that E. coli cells can be represented as cylinders, as a first approximation. This way, we could develop a 2D model of a transversal section of cells, using cylindrical coordinates.
Because of osmotic pressure differences, we assumed that the intracellular membrane is pushed against the -perfectly circular- peptidoglycan layer. So, only outer membrane deformations have to be modeled.
The difference of osmotic pressure between the intra-cellular environment and the periplasm, and between the periplasm and the extra-cellular environment comes notably from the turnover of peptidoglycan molecules [1]. This hypothesis has been made by Zhou & Doyle [2]
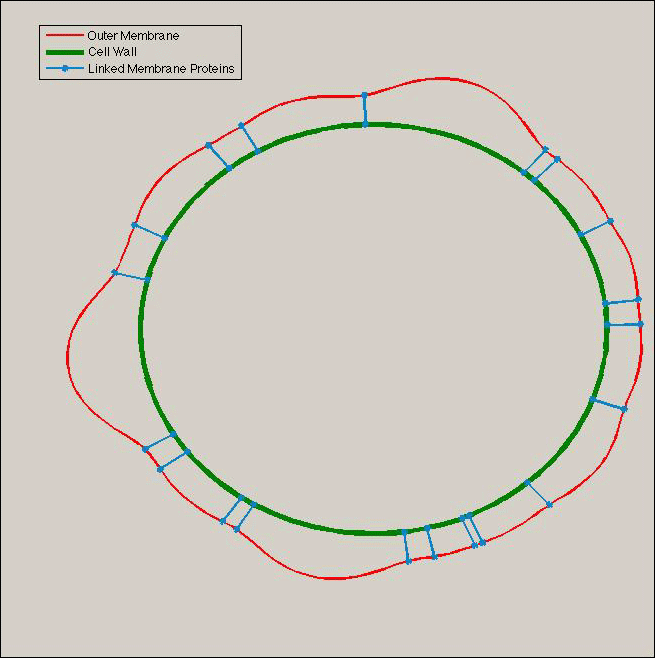
A last important assumption is that the outer membrane possess a non null intrinsic curvature. This comes from the presence of lipopolysaccharides (LPSs) in the outer membrane. The extracellular sugar extensions of LPSs create mutual attraction forces and thus curb the membrane [Greg: ref here]. This situation is depicted in the figure below.
To model membrane deformation, we use the equation proposed by Ou-Yang and Helfrich [3].
After simplifications, we obtain the following equality.
In this equation, γ is the variable membrane curvature, Δp is the osmotic pression difference, c0 is the membrane intrinsic curvature, and other parameters are as described in Zhong-can and Helfrich [3].
A formal connection between the membrane curvature γ and the cylindric coordinate variables r and θ can be obtained by the following polar curvature simplification approximation:
where
Lastly, by combining the two equations given above, we obtain the following set of differential equations describing membrane deformations:
Considering that we have low concentrations we can obtain a simpler formula analogue to the perfect gases law:
Finaly we have:
Here we observe that the model is depending of the volume V which will stabilized the equation and totally define all the parameters of the system.
In addition, we decided to model the role of the Tol/Pal system as boundary condition for the system of differential equations : cluster of Tol-Pal are considered as a point with a radius equal to peptidoglycan's one plus the length of the protein. Furthermore, as the surface is closed, we must impose the fact that r(0)=r(2π) to account for closing the vesicle.
Modeling Tol/Pal diffusion
Tol and Pal are membrane proteins which are located respectively in the outer and the inner membrane. Tol and Pal proteins interact with each other, forming Tol/Pal complexes. By acting like press studs binding the inner and outer membranes, thus stabilizing the outer membrane using the peptidoglycan rigidity, the Tol/Pal complexes play a central role to preserve membrane integrity [3].
The diffusion of proteins in these lipid bilayers can be modeled by Brownian motion. This diffusion model gives the probability law for the location of Tol and Pal in the membranes.
The following three equations model the Brownian motion of Tol, Pal and Tol/Pal complexes, represented as particles.
In the above equations, CX denotes the concentration of protein X, and DX denotes the constant kinetic coefficient associated to X. The kTolPal and k*TolPal denote the reaction constants for Tol-Pal complexation. In the last equation, Φ is an unknown function representing the Tol-Pal complex motility. However, because the Tol-Pal complex is significantly larger than the other proteins, and is doubly anchored in membranes, we made the assumption that the mobility of Tol-Pal complexes is negligable in comparison to the mobility of isolated Tol and Pal molecules. Stated differently, we set Φ to zero. Lastly, additional constraints on Tol/Pal diffusion have been added to enforce a constant distance between Tol and Pal proteins.
In the above equations, the laplacians capture the non-homogeneous molecular diffusion on non-flat membranes.
Indeed, they link the evolution of protein concentrations with the local shape of the membranes, since we know that on a two dimensional space:
where x and y are the coordinate of the surface and where the different partial derivatives are depending on the cartesian coordinates of the surface we are evolving on.
Unequal osmotic pressures create small blebbing
Using the equations for membrane deformation, we can compute numerically the shape of the outer membrane at steady state under various assumptions. If we assume that Tol/Pal complexes acts like press studs locally imposing a fixed distance between the two membranes, and that their initial distribution in the membrane is not totally homogeneous, then we obtain results of the following type.
- Shape at equilibrium of the outer membrane presenting blebs (red) resulting from osmotic pressure differences and with Tol/Pal complexes locally imposing a fixed distance between the inner (green) and outer membranes.
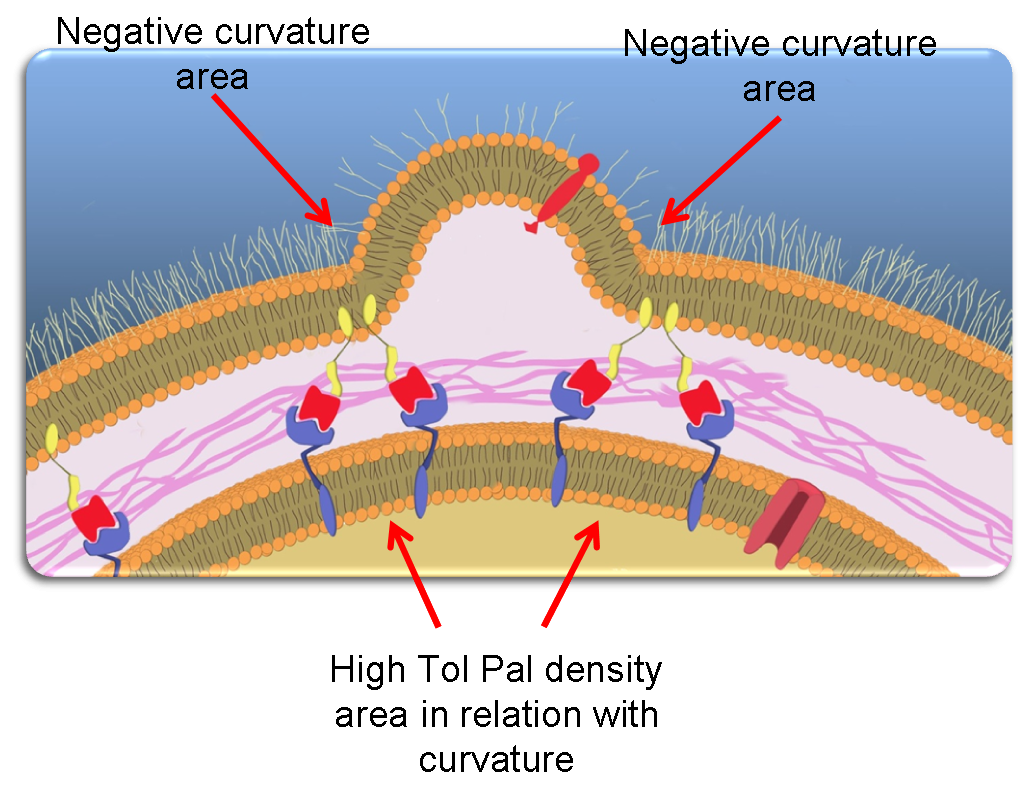
Tol/Pal accumulates at the basis of nascent blebs
The value of the Laplacian operators used to model Tol and Pal diffusions in the membranes (see equations above) depends on the membrane curvature: in non-flat membranes, the "efficiency" of the diffusion depends on the direction. In fact, molecules anchored in the outer membrane, like Pal, diffuse less efficiently in regions of negative curvature, and consequently tend to accumulate in these regions. This result is corroborated by recent experimental findings showing that “negative membrane curvatures [act] as a cue for sub-cellular localization of a bacterial protein” [9].
[Ca serait vraiment bien si on pouvait avoir un resultat de simulation qui montre cela! Meme si on ne prend pas tout en compte: on veut juste montrer que des particules sur une membrane non plate s'accumulent dans les regions courbes]
Most notably, we can thus assume that Pal molecules accumulate at the basis of blebs.
This naturally leads to an increase of Tol-Pal complexes formation in these regions.
Lastly, because we additionally assumed that these large complexes diffuse less efficiently than Tol and Pal alone, we finally obtain that Tol-Pal complexes accumulate at the basis of the blebs.
This is depicted in the following picture.
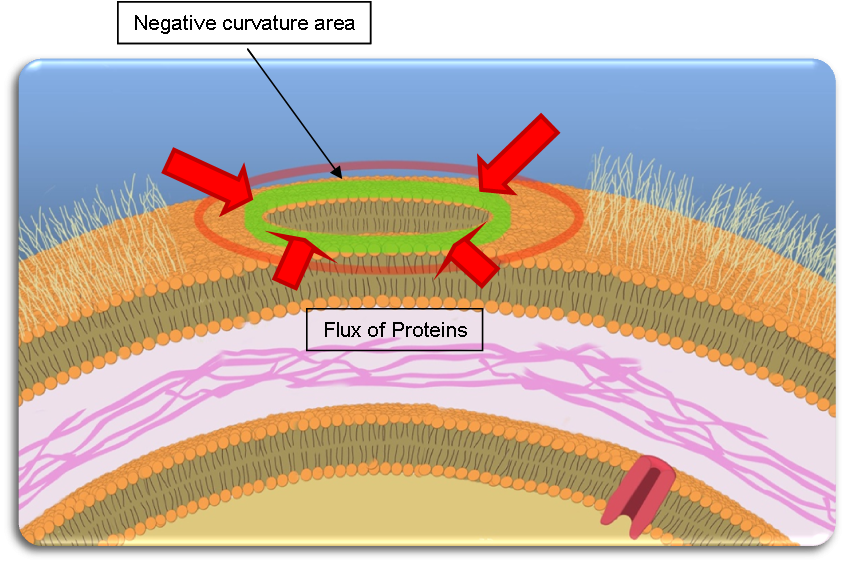
Rings of accumulated Tol/Pal constricts blebs basis
- In those regions the probability of linking between Pal and Tol is increased which enhances the local membrane stability and contributes to enlarge the region re-association with the peptidoglycan, the border between the blebbing and the membrane is going to vanish and the vesicle to detach itself from the surface. This reinforcement process driven by Brownian motion can explain the vesiculation. When there are too few proteins we can assume the creation of a vesicle at germinal states (called blebbing). But as the border between the blebbings and the protein rich area curvature is highly negative, the quantity of Tol-Pal proteins in this borders increases enlarging the region toward the centre of the blebs and are zippering back the membrane to the peptidoglycan . Then two different options can be considered: the blebbing is too small and then the proteins are “zippering” back the blebs. But if the bleb is big enough the zippering became a separation between the vesicle and the bacteria.
References
1 1991 - Lipowsky - The conformation of membranes, Nature, 349(6309):475-481
2 2008 - Park & Uehara - How bacteria consume their own exoskeletons, Microbiol Mol Biol Rev, 72(2):211-227
3 1998 - Zhou et al - On the origin of membrane vesicles in gram-negative bacteria, FEMS microbiology letters, 163(2):223-228
4 1987 - Ou-Yang & Helfrich - Instability and deformation of a spherical vesicle by pressure, Phys. Rev. Lett., 59:2486-2488
5 1995 - Fattal et al - The vesicle-micelle transition in mixed lipid-surfactant, Langmuir, 11:1154-1161
6 1977 - Harbich et al - Optical observation of rotationally symmetric lecithin vesicle shapes, J. Physique, 38:727–729
7 2009 - Deatherage et al - Biogenesis of bacterial membrane vesicles, Mol Microbiol, 72(6):1395-1407
8 2005 - Kuehn & Kesty - Bacterial outer membrane vesicles and the host pathogen interaction, Genes & Dev, 19:2645-2655
9 2009 - Kumaran & Losick - Negative membrane curvature as a cue for subcellular localization of a bacterial protein. PNAS USA, 106(32):13541-13545
Draft
Unequal osmotic pressures create small blebs
Simplified approach: without brownian motion of the intermembrane Tol-Pal links
- In the following we first focus on a model without brownian movement of the Tol-Pal links which are considered to be immobilized and randomly distributed over the E.coli membrane. We look also here at a simplified one dimensional membrane. Our aim is to get a realistic visual representation of the equilibrium shape of the outer membrane for a given osmotic pressure difference. In one dimension and in polar coordinates the equation describing the membrane conformation given by Zhong-can and Helfrich [Phys. Rev. Lett. 59 (1987) 2486] can be written as follows :
- Where H is the mean gaussian curvature and K is the Gaussian curvature :
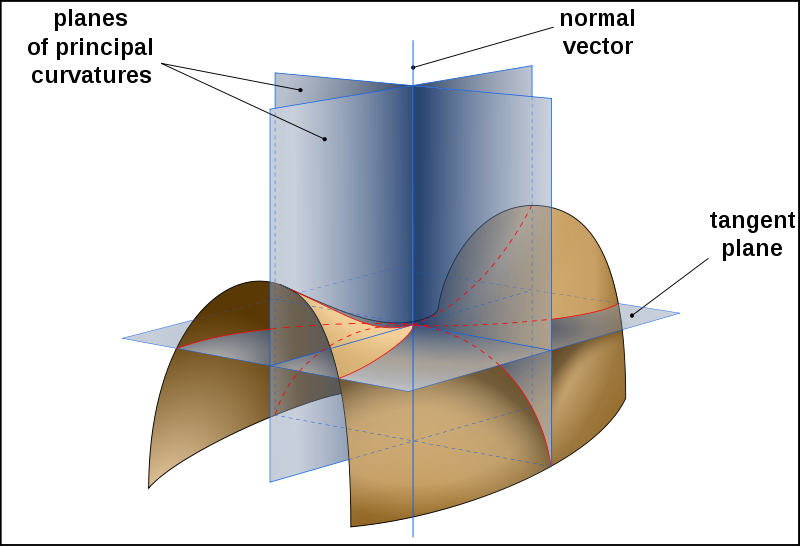
- The principal curvatures of a surface on the point M are defined as the minimum (c1) and the maximum (c2) curvatures at this position of the curves described by cuting the surface with plans containing the normal direction at this point.
Principal curvature on a given surface [http://en.wikipedia.org/wiki/Principal_curvature#top| extracted from an article on Wikipedia]
- We first simplified the membrane equation to a 2 dimensional equation system based on a polar curvature simplification approximation :
- the curvature in polar is where
- Due to cylindrincal symetry the principal curvatures are always equal to the curvature in the perpendicular plane of the cylinder and the curvature in his axis so the mean and gaussian curvatures can be written as:
- indeed we have in those hypothesis:
- the osmotic pressure can be written in this way:
- Considering that we have low concentrations we can obtain a simpler formula analogue to the perfect gases law:
- Finaly we have:
- Here we observe that the model is depending of the volume V which will stabilized the equation and totally define all the parameters of the system.
- With these relations the membrane equation becomes:
- In addition, we decided to model the role of the Tol/Pal system as boundary condition for the system of differential equations : cluster of Tol-Pal are considered as a point with a radius equal to peptidoglycan's one plus the length of the protein. Furthermore, as the surface is closed, we must impose the fact that r(0)=r(2π) to account for closing the vesicle.
- The integration of the polar membrane equations gives the following typical simulation results:
- Equilibrium shape of the outer membrane presenting blebbing (red) with immobile Tol-Pal links fixed to the inner membrane (green) assumed to be cylindrical, obtained with an increase of the periplasm pressure.
The lipid surface conformation
- The Lipid conformation of the outer membrane is a well known problem: at 35°c the lipid bilayer behaves like a liquid which conformation character is ruled by an energy called the bending energy (R. Lipowsky, The Conformation of Membranes, Nature 349 (1991) 475-481). This energy represents the fact that the lipid bilayer will search a special conformation depending on the shape and the chemical properties of its constituents. In order to explain the way lipids organize together we need an expression for the membrane bending energy. This is given by :
- E is the energy of a whole lipid bilayer (or monolayer). Kb and Kg are Bending and Gaussian moduli which can be obtained by experiments. γ0 is the intrinsic curvature of the outer membrane which describes the local form of a lipid bilayer when it is at is lowest state of energy ,the more stable. γm and Hg are the mean curvature and the gaussian curvature( see Helfrich [Z. Naturforsch. C 28 (1973) 693] ). dS is a surface infinitesimal element and the previous formula relates how the local surface energy varies with the local mean curvature and the Gaussian curvature. Let us first calculate the energy of two different shapes of membranes, (i) a model of the shape of E. coli before budding, and (ii) after budding of a vesicle.
- (i) We consider the shape of E.coli as a cylinder of radius r =0.3.
- This is a simplified shape based on the heuristic fact that in septa where the vesicle will be constituted principally with lipids of higher bending energy. In fact this model is just a first approach to determine range of parameters and could be developed in a more sophisticated way later.The aim of this first representation is to estimate this energy in the division region of E.coli before division. With this approximation γm = 1/2r.
- Thus for the E.coli lipids membrane the bending energy per aera is:
- (ii) For the vesicles we consider their basic shape as a sphere of rayon r’ so the bending energy by lipid area units is:
- Thus as the area of a sphere is known and is independent of the location on the surface we can write:
- The energy of the same membrane area in E.coli is:
- The relations can provide a basic vision of the statistical repartition of vesicles in case of absence of integrity control system in the outer membrane.
- Ee is the potential energy of the lipid area in E.coli outer membrane before construction of a vesicle and Ev is the energy of the same lipid area but in the conformation after budding including a vesicle shape. So the energy which must be given to the whole system to create a vesicle is:
Mettre une courbe expliquant ceci
- We can suppose that the most easily created vesicles will be the ones which require a minimum energy. By derivation we find that the minimum is obtain for:
- Hence as we know that the range of created vesicles radii is 25 nm to 175nm we can suppose that the r’ is somehow about 100 nm. This leads us to an estimation of the outer membrane intrinsic curvature:
- Which is realistic in the order of magnitude
- In fact we know that the E.coli lipid bilayer is built of distinct types of lipids: Lippopolysacharides (LPS) and simple phospholipids. LPS are located in the exterior lipid layer of the outer membrane. The others are located in the interior lipid bilayer. Moreover, those LPS present a sugar extension toward the medium. Those sugars can bind to each other. So we can assume that they are going to create clusters and to curve the membrane toward the exterior of E.coli.
- This part was dedicated to a first approach of the membrane shape and its characteristics introducing some concept of lipid membrane physics. It enable us to find a range value for one important parameter.
"Tol-Pal proteins diffusion"
- Tol and Pal are membrane proteins which are located respectively in the outer and the inner membrane. The diffusion of proteins in those lipid bilayers can be modelled by a probabilistic Brownian movement. This diffusion model gives us the law of probability for the location of Tol and Pal on the membranes. It has been observed that the Tol and Pal proteins interact with each other, which is linked to the membrane stability: indeed the Tol and Pal will bind inner and outer membrane and furthermore stabilize the outer membrane using the peptidoglycan rigidity.
Treatment including brownian motion of the intermembrane Tol-Pal linked proteins combined with simple Pal and Tol proteins
- We will now add to the Tol and Pal proteins motion the Tol-Pal binded proteins between the cell outer and inner membranes Brownian motion. This motion links the local concentration of proteins with the shape of the membrane they are included in. The diffusion of the whole particles are described by the three diffusion equations :
- The D coefficients are constants which give the kinetic for the concentration C.
- The Laplacian of P explains the fact that the concentration of proteins like Pal increased in regions of negative curvature. Such a model can explain some recent observations [Kumaran & Losick] “negative membrane curvatures as a cue for sub-cellular localization of a bacterial protein”.
- According to this we can assume that the Pal will be confined to region with negative curvature.
- In those regions the probability of linking between Pal and Tol is increased which enhances the local membrane stability and contributes to enlarge the region re-association with the peptidoglycan, the border between the blebbing and the membrane is going to vanish and the vesicle to detach itself from the surface. This reinforcement process driven by Brownian motion can explain the vesiculation. When there are too few proteins we can assume the creation of a vesicle at germinal states (called blebbing). But as the border between the blebbings and the protein rich area curvature is highly negative .the quantity of Tol-Pal proteins in this borders increases enlarging the region toward the centre of the blebs and are zippering back the membrane to the peptidoglycan . Then two different options are expectable: the blebbing is too small and then the proteins are “zippering” back the blebs. But if the bleb is big enough the zippering became a separation between the vesicle and the bacteria.
Periplasmic osmotic pressure increase
- The osmotic pressure in the periplasm is the same that the medium pressure in normal time. But during the division period of the bacteria the peptidoglycan is degraded to be recycled in a new cell wall. During this phenomenon of turn-over a part of the peptidoglycan is released in the periplasm which increased its osmotic pressure.
- Thus, we can consider that if there is not enough Tol-Pal linked proteins the outer membrane will distord to create a beginning of vesicle. But in this part of the membrane the tol pal proteins will not have the possibility to bind themselves and they will be free to diffuse in other parts of the membranes. The surface shape will guide the proteins to the border of the vesicle and stabilized the shape of the vesicle.
 "
"