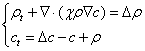Team:Aberdeen Scotland/modeling/pde
From 2009.igem.org
(→Discontinuous Galerkin Finite Element Method) |
(→Discontinuous Galerkin Finite Element Method) |
||
| Line 59: | Line 59: | ||
=== Discontinuous Galerkin Finite Element Method === | === Discontinuous Galerkin Finite Element Method === | ||
| - | THe Finite Element Method is a numerical technique for the solution of PDE's by discretising the domain over which the PDE is solved into finite "elements". The | + | THe Finite Element Method is a numerical technique for the solution of PDE's by discretising the domain over which the PDE is solved into finite "elements". The discretised domain is then termed the "mesh". Elements are interpolated by polynomial <i>basis functions</i> which serve to approximate the equation over the element without allowing errors in intermediate calculations to accumulate and render the final output meaningless. |
| + | |||
| + | <i>Discontinuous Galerkin</i> methods are an augmented family of Finite Element Methods developed by the Russian Engineer, Boris Galerkin. They are superior to other finite element methods for several reaons, including - but not restricted to - local, element wise mass conservation and flexibility to choose non- and high order polynomial bases. | ||
<html> | <html> | ||
Revision as of 12:15, 18 August 2009
University of Aberdeen - Pico Plumber
Contents |
Introduction
It was realised quite soon into the project that upon modelling the Inner Dynamics of the system, the individual modules could be collimated in to a single Partial Differential Equation – hereafter referred to as PDE – which would accurately describe the evolution of the system in space and time.
A PDE model was an excellent “next step” for our modelling effort – and although a physically meaningful model could not be generated; the following describes a concise modelling methodology which would merit implementation outside of iGEM – or indeed, in future iGEM competitions.
The Keller-Segel Chemotaxis system is a set of two coupled Nonlinear PDE’s; Parabolic except for a mixed Hyperbolic-Elliptic term in the cross-diffusive flux. The terms “Parabolic”, “Hyperbolic” and “Elliptic” refer to the number of boundary conditions the system must satisfy – the dependence on which defines (or “sets”) the behaviour of the system.
Where (insert pho_grad_c) is the cross-diffusive flux
The Keller-Segel system was perfect for modelling our PicoPlumber modules, inasmuch as Quorum Sensing could be effectively integrated into the formulation[1]. This allowed the advantage of analysing the dynamical evolution of the system in space & time - and in regard to the Internal Dynamics.
The following is an account of our researches into utilising these powerful Mathematical tools to describe our system.
One-Dimensional Diffusion Equation
As PDE’s are a challenging and actively-researched topic in Mathematics[2-3]; our modelling effort began by solving a much simpler problem by way of introduction to the field.
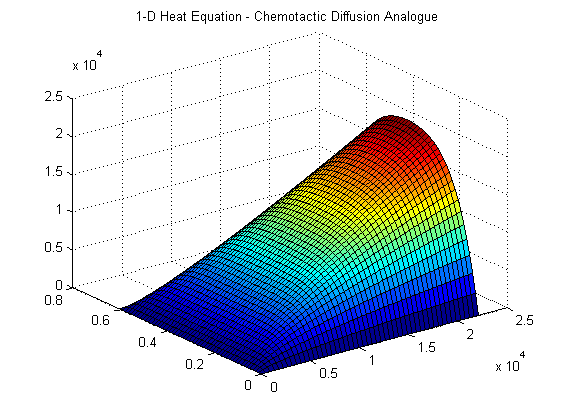
The one-dimensional Heat Equation is the classic introduction to Partial Differential Equations. It was modelled by utilising an Implicit Finite Difference method of our own composition. This allowed us to attain an aptitude for tackling the more difficult Keller-Segel system to come.
The Heat Equation and the Diffusion Equation of our chemo-attractant shared the same mathematical formulation – differing in fact, by the choice of the constant k – and so this introduction still retained a Biological pertinence.
Keller-Segel System for Chemotaxis
As mentioned above, the Keller-Segel System for Chemotaxis is the set of coupled Nonlinear PDE's which describe chemotactic motion. The mixed Hyperbolic-Elliptic term endows the system with rich behaviour – but also renders it insoluble by elementary Numerical Methods[footnote1].
In searching for a more advanced numerical method, Discontinuous Galerkin Finite Elements were found in Systems Biology literature[4]. to have successfully modelled the system and identified parametric instabilities.
In their award-winning paper[5]. , Hillen and Painter describe augmentations to the standard Keller-Segel System, hereafter referred to as the "Minimal Model". These augmentations account for effects such as density- and signal-dependent sensitivity, nonlinear diffusion and cell-growth & multiplication. The following documents the theoretical knowledge necessary to create a numerical algorithm to solve the system - which may be undertaken on a "Next steps" basis.
Minimal Model
The Chemotactic Minimal Model is the simplest "chassis" for describing a bacterial population chemotaxing towards a chemoattractant. It is of the form
where ![]() is the bacterial density,
is the bacterial density, ![]() the concentration of the chemoattractant and
the concentration of the chemoattractant and ![]() ,
, ![]() their respective time derivatives.
their respective time derivatives.
In Ephsteyn and Kurganov[4], the aforementioned Discontinuous Galerkin Finite Element Method is applied to successfully solve the system. The following will provide an abridged summary of the method, covering all elements necessary to implement the numerical method.
Discontinuous Galerkin Finite Element Method
THe Finite Element Method is a numerical technique for the solution of PDE's by discretising the domain over which the PDE is solved into finite "elements". The discretised domain is then termed the "mesh". Elements are interpolated by polynomial basis functions which serve to approximate the equation over the element without allowing errors in intermediate calculations to accumulate and render the final output meaningless.
Discontinuous Galerkin methods are an augmented family of Finite Element Methods developed by the Russian Engineer, Boris Galerkin. They are superior to other finite element methods for several reaons, including - but not restricted to - local, element wise mass conservation and flexibility to choose non- and high order polynomial bases.
 Back to Hill Input Functions Back to Hill Input Functions
|
Continue to Chemotaxis 
|
References
[1] Hillen T, Painter KJ, "A user's guide to PDE models for Chemotaxis" J Math Biol. 2009 Jan;58(1-2):183-217. Epub 2008 Jul 15.
[2] Oxford Centre for Nonlinear PDE. http://www.maths.ox.ac.uk/groups/oxpde/
[3] The Maxwell Institute: Centre for Analysis and Nonlinear PDE's. http://www.maxwell.ac.uk/PDEs/
[4] Epsteyn Y, Kurganov A, New Interior Penalty Discontinuous Galerkin Methods for the Keller–Segel Chemotaxis Model. J. Numer. Anal. Volume 47, Issue 1, pp. 386-408 (2008)
[5] Faculty of 1000 Biology. "A user's guide to PDE models for Chemotaxis" Importance recognition. http://f1000biology.com/article/id/1126950
 "
"